Mock test 1 solutions

Part A: Short-answer type questions

The values of $k$ for which the line $y=k x$ intersects the parabola $y=(x-1)^{2}$ are
(a) $k \geq-4$.
(b) $k \leq 0 $.
(c) $-4 \leq k \leq 0$.
(d) $k \geq 0$ or $k \leq-4$.
Sol.
(d) Equating $k x=(x-1)^{2}$, we get $x^{2}-(k+2) x+1=0$. The discriminant is $(k+2)^{2}-4=k(k+4) \geq 0$ for $k \geq 0$ or $k \leq-4$.
Let $\operatorname{gcd}(a, b)=1$, then $\operatorname{gcd}\left(a+b, a^{2}-a b+b^{2}\right)=$
(a) 2
(b) 1 or 2
(c) 1 or 3
(d) 2 or 3
Sol.
(c) Source: Madhava 2022..
Find the remainder when $\displaystyle \sum_{r=1}^{50} r! $ is divided by 12.
Sol.
Ans: 9. Terms after $3!$ are divisible by 12.
Find the number of solutions to the equation $\sqrt{1-\sin x}=\cos x$ in the interval $[0,5 \pi]$.
Sol.
Squaring both sides we get $1-\sin x=1-\sin^{2} x$ and thus $\sin x=0$ or $\sin x=1$. In $[0,5 \pi]$, we then have $x=0, \pi, 2 \pi, 3 \pi, 4 \pi, \pi / 2,5 \pi / 2,7 \pi / 2$. We need to reject the values $\pi, 3 \pi, 5 \pi$ as in these cases LHS=1 and RHS=-1. Hence number of solutions is 6 .
The number of real roots of the equation $x^6-x+1$ is:
(a) Zero.
(b) exactly 1.
(c) exactly 2.
(d) exactly 4.
Sol.
(a) Zero.
Alice has the five letters: A, B, C, D, E. How many ways can she rearrange the letters into three words? The order of the words matter. For example, "AB C DE" and "C AB DE" are different rearrangements.
Sol.
We can permute the letters is 5! ways. Each permutation can be split is $ {4 \choose 2} $ ways. Hence, the required number of ways is $120\times 6 = 720$.
Find the sum of the coefficients of the polynomial obtained after expanding and collecting the terms of the product $\left(5x^{2}-5x+1\right)^{10}\left(x^{4}-2x+1\right)^{20}$.
Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a continuous function such that $|f(x)-f(y)| \geq|x-y|$ for all real numbers $x, y$. Then which of the options below are true?
(a) $f$ is one-one
(b) $f$ is onto
(c) $f^{-1}$ may not exist
(d) $f^{-1}$ is continuous
Sol.
(a),(b) and (d). If $f(x)=f(y)$, then $|f(x)-f(y)|=0$ so $f$ is one-one. If $f(1)> f(0)$ the function is monotonically increasing. If $f(1)< f(0)$, then the function is monotonically decreasing.
Let $\left\{a_{n}\right\}$ and $\left\{b_{n}\right\}$ be two sequences of non-zero real numbers. We say that $\left\{a_{n}\right\}$ and $\left\{b_{n}\right\}$ are mostly equal if $\lim_{n \rightarrow \infty} \frac{a_{n}}{b_{n}}=1$. Which of the following sequences are mostly equal?
(a) $a_{n}=n-2\sqrt{n}, b_{n}=n$.
(b) $a_{n}=n^{2}+\sqrt[3]{n}, b_{n}=n$.
(c) $a_{n}=n!, b_{n}=n^{n}$.
(d) $a_{n}=\left(1+\frac{1}{n}\right)^{n}, b_{n}=e$.

Sol.
(a) and (d).
We have two identical cups denoted by M and W. Cup M contains a milk and cup W has equal amount of water in it. One spoon of milk is transferred to cup W and then one spoon of the mixture in cup W is transferred to cup M. Then which of the following is true?
(a) The amount of milk in cup W bigger than the amount of water in cup M.
(b) The amount of milk in cup W smaller than the amount of water in cup M.
(c) The amount of milk in cup W is equal to the amount of water in cup M.
(d) Can't say since it depends on the size of the spoon.

Sol.
(c) Source: 2021 Madhava.

Part B: Subjective questions

Clearly explain your entire reasoning. No credit will be given without reasoning. Partial solutions may get partial credit.

B1 (a) Find a four digit number which on division by 149 leaves a remainder of 17 and on division by 148 leaves a remainder of 29 .

B1 (b) Find all the primes $p$ such that $2^p+p^2$ is also prime.

Sol.

(a) Let $x$ represent the required four digit number. Thus $x=149 q_{1}+17$ and $x=148 q_{2}+29$. Since $x$ is a four digit number $7 \leqslant q_{1}, q_{2}<70$. Subtracting the above equations gives \begin{align*} 149 q_{1}-148 q_{2}&=12\\ 148\left(q_{1}-q_{2}\right)+q_{1}&=12 \end{align*} Hence, since $q_{1}-q_{2}$ is an integer its value must be zero, which gives $q_{1}=q_{2}=12$, and $x=149 \times 12+17=1805$.

(b) Note if $p>3$, then $p \equiv 1$ or $5 \bmod 6$. Then $p^{2} \equiv 1 \bmod 3$. As $p$ is odd, $2^{p} \equiv 2$ $\bmod 3$, so $p^{2}+2^{p}$ is divisible by 3 and thus not prime. Thus we only need to check the cases when $p=2$ and $p=3$, and we see that $p^{2}+2^{p}$ is only prime when $p=3\left(p^{2}+2^{p}=17\right)$.

B2. Three points $A, B$ and $C$ lie inside a circle whose radius is 1 cm. Show that $B C^{2}+C A^{2}+A B^{2}$ is less than or equal to 9 sq. cm.

Sol.

We may assume that points $A, B$ and $C$ lie on a circle and form a triangle. Further, we may restrict our triangles to those where $BC=AC$. The reason is given below.

Claim: The expression $BC^2+CA^2+AB^2$ has a maximum when $BC=AC$.
Proof:
Pick a point $C^\prime$ such that $AC^\prime = BC^\prime$. We will show that triangle $ABC^\prime$ is a better choice than triangle $ABC$. Consider the figure shown below. \begin{align*} &A B^{2}=A C^{2}+B C^{2}-2 A C \cdot B C \cos \theta=A C^{\prime}{ }^{2}+B C^{t^{2}}-2 A C^{\prime} B C^{\prime} \cos \theta\\ &\text { Since } \quad \frac{1}{2} \mathrm{AC} \cdot \mathrm{BC}=\frac{\text { Area } \triangle \mathrm{ABC}}{\sin \theta} < \frac{\text { Area } \triangle AB\mathrm{C}^{\prime}}{\sin \theta}=\frac{1}{2} \mathrm{AC}^{\prime} \cdot \mathrm{BC}^{\prime}\\ &\text { we have } A B^{2}+A C^{2}+B C^{2}=2 A B^{2}+2 A C \cdot B C \cdot \cos \theta\\ &< 2 A B^{2}+2 A C^{\prime} \cdot B C^{\prime} \cos \theta=A B^{2}+A C^{\prime 2}+B C^{\prime 2} \; \square \end{align*}

Similar argument can made to show that $AB=BC$ at the maximum value. Hence, the quantity $AB^2+BC^2+CA^2$ is maximized when the triangle $ABC$ is equilateral. When this happens each side has length $2\cos 30^\circ=\sqrt{3}$ cm. The statement follows.

B3. We have three colors: red, blue and green. In how many ways can we color the vertices of an octagon such that no two adjacent vertices have the same color? A valid coloring of the octagon is shown below. Adjacent vertices are connected by a line segment.

Remark. If we were coloring a triangle instead of an octagon, there would be 6 ways to do it. The first vertex can be colored in 3 ways, the second vertex can be colored 2 ways and the color of the third vertex would be fixed.

Sol.

For any $n$-polygon with four or more sides, we consider two cases.
Case 1: Vertex 1 and vertex $n-1$ are different colours. Then this means that vertices 1 to $n-1$ can be coloured in all ways possible for a $n-1$ gon and the colour of vertex $n$ is fixed.
Case 2: Vertex 1 and vertex $n-1$ are the same colour. Then vertices 1 to $n-2$ can be coloured in all ways possible for a $n-2$ gon, and then there are 2 ways to colour vertex $n$. We define $a_{n}$ as the legal colourings of an $n$-gon. Then $a_{n}$ can be recursively defined as \[ a_{n}=a_{n-1}+2 a_{n-2} \] An edge or a triangle can be colored in 6 ways, so $a_2=a_3=6$. Therefore, for $n=8, a_{n}=258$.

B4 (a). Simplify $ \sqrt[3]{2+\sqrt{5}} + \sqrt[3]{2-\sqrt{5}}$.

B4 (b). Which is larger: $\sqrt[8]{8!}$ or $ \sqrt[9]{9!} $?

Sol.

(a) Let $x= \sqrt[3]{2+\sqrt{5}} + \sqrt[3]{2-\sqrt{5}}$. Let $A$ and $B$ be the two summands, so $x=A+B$. Using the identity $(A+B)^3 = A^3 + B^3 + 3AB(A+B)$, we get: \begin{align*} x^{3} &=(2+\sqrt{5})+3(\sqrt[3]{2+\sqrt{5}} \cdot 3 \sqrt[3]{2-\sqrt{5}})(x)+(2-\sqrt{5}) \\ &=4+3 \sqrt[3]{(-1)} x \\ &=4-3 x \end{align*} Hence, $x^3+3x-4=(x-1)(x^2+x+4)=0$. The only real solution to the equation is $x=1$.
(b) We that that $8! < 9^8$. Multiply both sides of the inequality with $8!^8$. We get: \[ (8!)^9 < 9^8\cdot(8!)^8 = (9!)^8 \] Take the 72 and root of both sides \begin{align*} &(8 !)^{9 / 72}<(9 !)^{8 / 72} \\ &\text { 1.e. } \sqrt[8]{8} !< \sqrt[9]{9} ! \end{align*}

B5.

Suppose $f$ is a differentiable function from the $\mathbb{R}$ into $\mathbb{R}$. Suppose $f'(x) > f(x)$ for all $x \in \mathbb{R}$ , and $f(x_0) = 0$ for some $x_0 \in \mathbb{R}$. Prove that $f(x) > 0$ for all $x > x_0$ .
Show that the equation $Ae^x = 1 + x + \frac{x^2}{2}$ , where $A$ is a positive constant, has exactly one real root.

Sol.

(i) Let $g(x) = e^{-x} f(x)$ . Then, $g'(x) =e^{-x} (f'(x) — f(x)) > 0$ . As $g$ is an increasing function, so we have $g(x)= e^{-x} f(x) \geqslant 0$ for $x >x_0$ , and the conclusion follows.

(ii) Let $f : \mathbb{R} \to \mathbb{R}$ be defined by $f(x) = Ae^x - 1 - x - \dfrac{x^2}{2}$.

Now, $f(x) \to -\infty$ as $x \to -\infty$ , and $f(x) \to +\infty$ as $x \to +\infty$ . Hence, as $f$ is continuous, it has at least one real root, say $x_0$. Observe that : $$f'(x) = Ae^x - 1 - x > Ae^x - 1 - x - \frac{x^2}{2} = f(x)\qquad\forall~ x\in\mathbb{R}$$ Thus, by part (i), we deduce that $f$ has only one real root, viz. $x_0$.
Source: UC Berkeley Ph.D Entrance Exam, Spring 1987

B6. $ABCD$ is a cyclic quadrilateral with side lengths as follows. $AB = 6$ cm, $BC = 12$ cm, $CD = 3$ cm and $DA = 6$ cm. Find the length of $EF$ in the figure shown below.

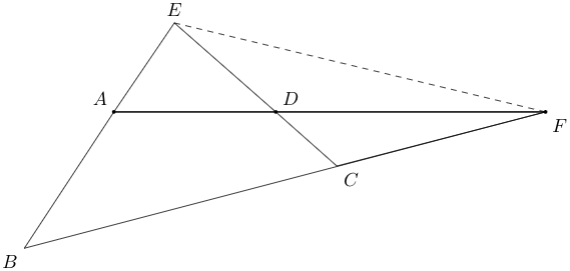
Sol.

Ans. $10\sqrt{2}$.
The key is to observe that $ \Delta BEC \sim \Delta DEA $. Likewise, $\Delta AFB \sim \Delta CFD $.
Lemma 1. $\triangle BEC \sim \Delta DEA $

Proof: Since $ABCD$ is a cyclic quadrilateral, the opposite angles sum to $\pi$. Let $\angle EBC=\theta$. Hence, $ \angle ADC = \pi-\theta$, so $\angle EDA = \theta $.

Lemma 2. $AE=4$ cm and $DE=5$ cm.

Proof: Since $DA:BC=1:2$ the scaling factor between similar triangles $\Delta BEC$ and $\Delta DEA$ is 2. Let $AE=p$ and $DE=q$. Then we have: \begin{align*} AB&=BE-AE\\ &=2DE-AE\\ &=2q-p \end{align*} Also, $CD=2p-q$. So we have: \begin{align*} 2q-p &= 6 \\ 2p-q &= 3 \end{align*} Solving for $p$ and $q$, we get $p=4$ and $q=5$. $\;\;\;\square$

Similarly we have $FC=8$ cm and $FD=10$ cm.
Let $\angle B=\theta$. Then $\angle F D E=\pi-\theta$. Apply the Law of Cosines to $\triangle E B F$ to get: \[ E F^{2}=B E^{2}+B F^{2}-2 B E \cdot B F \cdot \cos \theta=10^{2}+20^{2}-2 \cdot 10 \cdot 20 \cos \theta=500-400 \cos \theta \] and to $ \triangle E D F$ to get \[ E F^{2}=D E^{2}+D F^{2}-2 \cdot D E \cdot D F \cos (\pi-\theta)=5^{2}+10^{2}-2 \cdot 5 \cdot 10 \cos \theta=125+100 \cos \theta \] Solving for $E F^{2}$, we get $E F^{2}=200$. So $EF=10\sqrt{2}$.