Mock test #1

Part A: Short-answer type questions

For this part, answers must be written without any explanation.

The values of \(k\) for which the line \(y=k x\) intersects the parabola \(y=(x-1)^{2}\) are
(a) \(k \geq-4\).
(b) \(k \leq 0 \).
(c) \(-4 \leq k \leq 0\).
(d) \(k \geq 0\) or \(k \leq-4\).
Let \(\operatorname{gcd}(a, b)=1\), then \(\operatorname{gcd}\left(a+b, a^{2}-a b+b^{2}\right)=\)
(a) 2
(b) 1 or 2
(c) 1 or 3
(d) 2 or 3
Find the remainder when \(\displaystyle \sum_{r=1}^{50} r! \) is divided by 12.
Find the number of solutions to the equation \(\sqrt{1-\sin x}=\cos x\) in the interval \([0,5 \pi]\).
The number of real roots of the equation \(x^6-x+1\) is:
(a) Zero.
(b) exactly 1.
(c) exactly 2.
(d) exactly 4.
Alice has the five letters: A, B, C, D, E. How many ways can she rearrange the letters into three words? The order of the words matter. For example, "AB C DE" and "C AB DE" are different rearrangements.
Find the sum of the coefficients of the polynomial obtained after expanding and collecting the terms of the product \(\left(5x^{2}-5x+1\right)^{10}\left(x^{4}-2x+1\right)^{20}\).
Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) be a continuous function such that \(|f(x)-f(y)| \geq|x-y|\) for all real numbers \(x, y\). Then which of the options below are true?
(a) \(f\) is one-one
(b) \(f\) is onto
(c) \(f^{-1}\) may not exist
(d) \(f^{-1}\) is continuous
Let \(\left\{a_{n}\right\}\) and \(\left\{b_{n}\right\}\) be two sequences of non-zero real numbers. We say that \(\left\{a_{n}\right\}\) and \(\left\{b_{n}\right\}\) are mostly equal if \(\lim_{n \rightarrow \infty} \frac{a_{n}}{b_{n}}=1\). Which of the following sequences are mostly equal?
(a) \(a_{n}=n-2\sqrt{n}, b_{n}=n\).
(b) \(a_{n}=n^{2}+\sqrt[3]{n}, b_{n}=n\).
(c) \(a_{n}=n!, b_{n}=n^{n}\).
(d) \(a_{n}=\left(1+\frac{1}{n}\right)^{n}, b_{n}=e\).
We have two identical cups denoted by M and W. Cup M contains a milk and cup W has equal amount of water in it. One spoon of milk is transferred to cup W and then one spoon of the mixture in cup W is transferred to cup M. Then which of the following is true?
(a) The amount of milk in cup W bigger than the amount of water in cup M.
(b) The amount of milk in cup W smaller than the amount of water in cup M.
(c) The amount of milk in cup W is equal to the amount of water in cup M.
(d) Can't say since it depends on the size of the spoon.

Part B: Subjective questions

Clearly explain your entire reasoning. No credit will be given without reasoning. Partial solutions may get partial credit.

B1 (a) Find a four digit number which on division by 149 leaves a remainder of 17 and on division by 148 leaves a remainder of 29 .

B1 (b) Find all the primes \(p\) such that \(2^p+p^2\) is also prime.

B2. Three points \(A, B\) and \(C\) lie inside a circle whose radius is 1 cm. Show that \(B C^{2}+C A^{2}+A B^{2}\) is less than or equal to 9 sq. cm.

B3. We have three colors: red, blue and green. In how many ways can we color the vertices of an octagon such that no two adjacent vertices have the same color? A valid coloring of the octagon is shown below. Adjacent vertices are connected by a line segment.

Remark. If we were coloring a triangle instead of an octagon, there would be 6 ways to do it. The first vertex can be colored in 3 ways, the second vertex can be colored 2 ways and the color of the third vertex would be fixed.

B4 (a). Simplify \( \sqrt[3]{2+\sqrt{5}} + \sqrt[3]{2-\sqrt{5}}\).

B4 (b). Which is larger: \(\sqrt[8]{8!}\) or \( \sqrt[9]{9!} \)?

B5.

Suppose \(f\) is a differentiable function from the \(\mathbb{R}\) into \(\mathbb{R}\). Suppose \(f'(x) > f(x)\) for all \(x \in \mathbb{R}\) , and \(f(x_0) = 0\) for some \(x_0 \in \mathbb{R}\). Prove that \(f(x) > 0\) for all \(x > x_0\) .
Show that the equation \(Ae^x = 1 + x + \frac{x^2}{2}\) , where \(A\) is a positive constant, has exactly one real root.

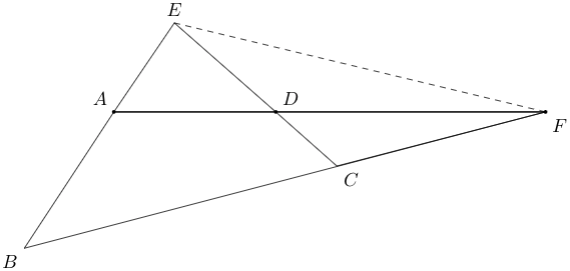
B6. \(ABCD\) is a cyclic quadrilateral with side lengths as follows. \(AB = 6\) cm, \(BC = 12\) cm, \(CD = 3\) cm and \(DA = 6\) cm. Find the length of \(EF\) in the figure shown below.