Mock test 5
Question Paper
Part A: Short-answer type questions
For this part, answers must be written without any explanation.
- There are three pastures of area 35 acres, 10 acres and 65 acres. On a certain date the owner places 17, 7 and 23 cows in the pastures, respectively. The grass in the first pasture is exhausted after 7 weeks, and that in the second after 4 weeks. For how long can the 23 cows be grazed in the third pasture?
Assume that initially there is the same amount of grass/unit area and that new grass grows at the same constant rate in all three pastures. - Find the shortest distance from the point \(A=(0,2)\) to the arc of the parabola \(y=x^2\) which is between \(x=0\) and \(x=1\).
- We have an \(n\times n\) grid of points, where \(n\) is an even number. There is a black spot at the center of the grid. In how many ways can we draw an axis-parallel rectangle with corners as the grid points such that the spot is inside the rectangle? An example of a rectangle is shown for a grid of size \(n=6\):
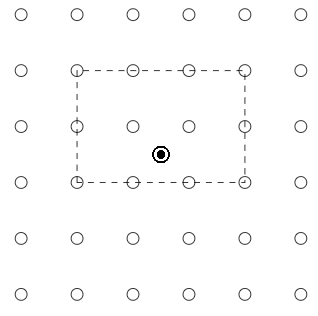
- Let \(A\) be a \(3 \times 3\) matrix with entries from the set \(\{-1 , +1\}\). Also, it is given that the first row and the first column of \(A\) contains only \((+1)\). Find the maximum value of determinant of \(A\).
- Evaluate : \(\displaystyle\int_0^{102} \sum_{k=1}^{100} \dfrac{\prod_{n=1}^{100}(x-n)}{x-k}\,\text{dx}\)
- Does there exist a real polynomial \(H(x)\) with integer coefficients such that \(H(13) = 21\) and \(H(50) = 122\)?
Consider two functions \(f\) and \(g\) defined as : \[ f(x) = \dfrac{1}{x+a} + \dfrac{1}{x+b} - \dfrac{1}{c_1}\quad~\&~\quad g(x) = \dfrac{1}{x+a} + \dfrac{1}{x+b} - \dfrac{1}{c_2} \] where \(a, b, c_1, c_2\) are real constants. Both \(f\) and \(g\) have the property that their roots are equal in magnitude, but opposite in sign, i.e. if \(\alpha\) is one root of \(f\) , then its other root is \((-\alpha)\) . Simlarly, if \(\beta\) is one root of \(g\) , then the other root of \(g\) is \((-\beta)\).
Let \(P_1\) denote the product of roots of \(f\) , and let \(P_2\) denote the product of two roots of \(g\). Find the value of \(\big(P_1 + P_2\big)\) , when \(a = 12\) , \(b = 13\) , \(c_1 = 147\) and \(c_2 = 187\) .Evaluate the following integral : \(\displaystyle\int_{0}^{2\pi} \frac{1}{3+\cos t}dt\)
We have a circular table with 6 chairs. Alice, Bob and Charlie each pick a random chair to sit down in. What is the probability that there are two empty chairs next to each person?
Given a complex number \(z\) such that \( z^{13}=1\), find all possible values of \( z+z^{3}+z^{4}+z^{9}+z^{10}+z^{12} \).
Part B: Subjective questions
Clearly explain your entire reasoning. No credit will be given without reasoning. Partial solutions may get partial credit.
B1. In how many ways can \(2^{100}\) be expressed as a sum of four squares of integers?
B2. Consider the following polynomial where \(a_1,\ldots,a_n\) are distinct integers. \[ r(x) = \left(x-a_{1}\right)^{2}\left(x-a_{2}\right)^{2}\left(x-a_{3}\right)^{2} \ldots \left(x-a_{n}\right)^{2}+1 \] Prove that \(r(x)\) cannot be written as the product of two other polynomials with integral coefficients.
B3. (i) Suppose \(f\) is a differentiable function from the \(\mathbb{R}\) into \(\mathbb{R}\). Suppose \(f'(x) > f(x)\) for all \(x \in \mathbb{R}\) , and \(f(x_0) = 0\) for some \(x_0 \in \mathbb{R}\). Prove that \(f(x) > 0\) for all \(x > x_0\). \(\;\;\;\) [5 marks]
(ii) Show that the equation \(Ae^x = 1 + x + \frac{x^2}{2}\) , where \(A\) is a positive constant, has exactly one real root. \(\;\;\;\) [5 marks]
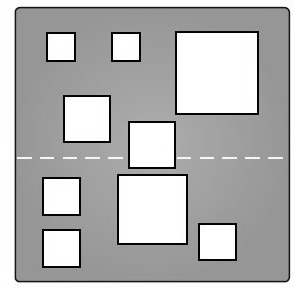
B4. We have a unit square made out of black paper. There are \(n\) axis-aligned white squares contained inside the black unit square. Let \(S\) denote the set of white squares. The squares in \(S\) are pairwise disjoint. Prove that there exists a horizontal line that intersects the unit square and passes through at most \( \sqrt{n} \) squares in \(S\).
You may assume that \(n\) is a perfect square. For example, the figure shows a unit square containing \(n=9\) white squares.
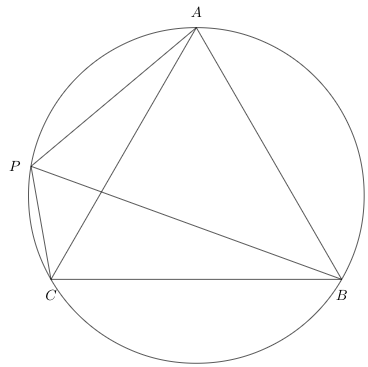
B5. \(ABC\) is an equilateral triangle and \(P\) is point on the circumcircle of \(ABC\). \(P\) is any point on the arc \(AC\). Prove that \(PB=PA+PC\).
B6. Let \(x\) be any real number and \(N\) be any integer \(>1\). Show that there exists a rational number \(p/q\), with \(p\) and \(q\) integers and \(0< q \leqslant N\), such that: \[\left|x-\frac{p}{q}\right| < \frac{1}{Nq}\]
For example, if \(x=\pi\) and \(N=10\), we can take \(p/q=22/7\). Then \(|\pi-22 / 7|<1/70\).